Spoiler Alert

We presented the PITA algorithm as a randomization tool to enhance generalization capabilities in Reinforcement Learning. Our experiment showed that PITA significantly improved the agent’s per- formance by increasing the amount of available training levels. However, we encountered diminishing returns at some point.

Good to Know

Having a good understanding of overfitting is important. Ideally, you also posses knowledge about Reinforcement Learning, although it is not mandatory. Most importantly you should bring enthusiasm for instructing artificial agents on how to navigate complex 3D environments such as video games. If this sounds like something you’re excited about, then this paper is for you.

Summarizing statement

Have you ever faced the problem of having to learn how to use a simulation engine for one of your Reinforcement Learning experiments? And perhaps did you even have to create several environments at once to combat overfitting? Then fear no more! With this paper, we unveil PITA, short for Procedural and Iterative Terrain Assembly - an algorithm that can significantly reduce the overhead of environment creation and randomization in MuJoCo. The paper provides an exhaustive introduction to PITA by explaining its core features and usage. Afterward, we perform a rigorous evaluation to showcase how PITA can help avoid overfitting and thus train agents that generalize well.

PITA – a Tool for Parameterized and Iterative Terrain Assembly in MuJoCo

by Gerrit York Bartels, Jakob Maximilian Dudek, Leonard Frommelt, Julian Blanke, Peter Keffer | Dec 11, 2024 | AI, Neuroinformatics

1. Introduction

At the core of supervised Machine Learning (ML) lies the imperative to train models for specific tasks, achieved through alignment with labeled data drawn from an existing source distribution. This data ideally captures the learning objective well, such that the model can generalize to unseen data from the target distribution. A major issue in ML is overfitting, which occurs when a model memorizes the training data instead of learning the underlying target distribution. For instance, a classifier model for animals might simply memorize a set of images of "dogs" rather than obtaining the ability to generalize to the concrete concept of "dog" (Russell & Norvig, 2020).

This type of problem also exists in the domain of Deep Reinforcement Learning (DRL, Zhang et al., 2018). DRL is similar to unsupervised learning in the sense that it does not use labeled data. Instead, an agent, represented as a neural network, is trained via Reinforcement Learning (RL) to learn a specific behavior for solving problems by interacting with the environment. Often, a specific environment instance is also referred to as a level, which is why we will use it synonymously in this work. A common testbed for RL is training an agent to win games. Risi and Togelius (2020) point out, that the widely used Arcade Learning Environment, a benchmark tool consisting of Atari games, only comprises fixed sets of levels with little randomization. Consequently, the authors argue that trained agents tend to overfit on single levels or event sequences. Also, Zhang et al. (2018) showed that DRL agents possess the capability to memorize explicit levels in comparable setups instead of learning to play a given game and generalize to new ones. In other words, the agents did not learn to generalize to the underlying data distribution but instead overfitted on the training data.

A lack of generalization also plays an essential role in the related research area known as sim2real. The goal is to train a model in a simulation environment (source domain) to be later used in the real world (target domain), for example, in autonomous driving. However, bridging the gap between simulation and reality poses a substantial challenge. This is because fitting on a restricted set of training data can lead to a lack of generalization and, thus, to poor performance in the real world, with potentially disastrous consequences (Andrychowicz et al., 2020; X. Chen et al., 2022).

In order to avoid this behavior, a training algorithm has to find a more general way to interpret this data. One angle from which this issue is tackled in current RL research is the randomization of the source domain. There are various approaches for Domain Randomization (DR), varying in complexity, use cases, and respective state of research. These usually entail the application of Procedural Content Generation (PCG), to avoid the necessity of hand-crafting environment instances from randomized parameters (Risi & Togelius, 2020).

In this work, we present PITA ¹, short for Procedural and Iterative Terrain Assembly, a framework for DR in simulated environments built in MuJoCo. MuJoCo ² (Multi-Joint dynamics with Contact, Todorov et al., 2012) is one of the most commonly used simulation engines for RL and robotics research (Kaup et al., 2024). It is currently maintained by Google DeepMind and has become freely available and open-sourced ³.

To offer a comprehensive overview, we will demonstrate the user-friendly nature of PITA, explain its current features, and quantify its effect on generalization using a classical navigation task. Our experimental framework involves a systematic comparison across conditions with respect to the agent’s performance on a held-out test dataset. Conditions were chosen to cover a broad range of available training levels. The core contributions of this work can be summarized as follows:

We present PITA as a new framework for generating randomized environments in the MuJoCo simulation engine that can be applied to various research setups.
We demonstrate PITA’s ease of use and explain its features in order to facilitate accessibility for researchers from diverse domains such as linguistics, psychology, or anthropology.
We show that stochastic generation of environments with PITA can be used to prevent undesired side effects, such as overfitting or lack of generalization.
We explore future directions that PITA could take and outline what further steps are needed to achieve a comprehensive evaluation.

2. Related Work

Within the domain of Reinforcement Learning research, there is a large interest in mitigating the risk of overfitting and enhancing the generalization capabilities of agents. A prominent example is the work of Zhang et al. (2018), in which they show that agents often overfit and have the capability of memorizing sets of levels instead of learning the game’s fundamental mechanics. This was done by introducing a new metric that uses sets of test levels that are disjunct from those used during training, similar to supervised ML. Examples in which this metric has been used comprise a variety of benchmarks for testing the generalization capabilities of RL or comparable policy learning algorithms in either 2D (Cobbe et al., 2019, 2020; Kanagawa & Kaneko, 2019) or 3D environments (Dai et al., 2022; Juliani et al., 2019). While these benchmarks and the conducted experiments offer great insights into the generalization capabilities of different RL approaches, they are limited to the analysis in their respective scenarios.

A closely related problem is that of Domain Transfer (DT). In DT, generalization should occur in a way that allows for the model to successfully cope with data that stems from a distribution other than the one underlying the training data. A common example of this is the problem of sim2real (Akkaya et al., 2019; Andrychowicz et al., 2020; X. Chen et al., 2022; Kontes et al., 2020; Weng, 2019). Here, RL agents for robot control are trained in simulations to collect the required training data in a feasible time without producing collateral damage. Simulations, however, are not able to completely capture the complexity of reality (e.g., there exists no model of collision of soft objects, no mathematical solutions for many dynamical systems, and numerical solutions are susceptible to chaos, etc.), and therefore, it constitutes a new domain. The agent, in effect, is fitted to the simulation domain and does not generalize well to the same problem setup in the real world.

In Johansen et al. (2019), a port of the Video Game Description Language (VGDL) to the Unity engine, called UnityVGDL, is introduced and evaluated as a training environment generator for RL. The authors point out that this port could be used as a procedural content generator in the future by coupling it with existing strategies for randomizing VGDL representations of games. However, to the best of our knowledge, this strategy has yet to be applied. While it allows for a more diverse adjustment of complexity than the previously mentioned PCG approaches, it is restricted by the underlying game description language. In a similar manner, Samvelyan et al. (2021) introduce MiniHack, a framework for procedurally generating 2D environments for RL. While the customization of level generation requires learning a mini-programming language specific to MiniHack, it can accelerate the process of environment creation. The Avalon Benchmark (Albrecht et al., 2022), on the other hand, provides procedurally generated RL environments for a range of predefined tasks in a 3D world simulated in the GODOT engine. However, due to the nature of benchmarks, it is focused on comparability and does not allow for the use of custom RL tasks.

In Risi and Togelius (2020), a comparison of Domain Randomization approaches for RL is presented. They establish a taxonomy (which builds upon Weng, 2019) that divides DR techniques into three categories, allowing us to embed our own work into this context.

Uniform Domain Randomization creates or randomizes a level based on uniform samples from a predefined range of parameters. The PCG aspects of the aforementioned benchmarks can be seen as examples of this approach. Additionally, they serve as showcases for PCG’s ability to prevent overfitting on subsets of levels. Uniform Domain Randomization is a core functionality of PITA.

Automatic Domain Randomization iteratively increases the ranges from which parameters for level generation get sampled. This not only lowers the chances of overfitting on the training examples but ideally also leads to zero-shot domain adaptation, e.g. by transferring from a simulated environment to the real world. Most notably, this was achieved in Akkaya et al. (2019) by bridging the sim2real gap in a zero-shot fashion.

Guided Domain Randomization changes the randomization distributions according to a second model. This second model is trained alongside the RL agents with the training objective of finding the most helpful areas of the environment randomization space. There is a multitude of approaches for Guided Domain Randomization, including Active Domain Randomization (Mehta et al., 2020), Compositional Design of Environments (CoDE, Gur et al., 2021), enhanced Paired Open-Ended Trailblazer (POET, Wang et al., 2020), and several methods that use Bayesian optimization on the posteriors of level distributions such as Bayesian Domain Randomization (BayRn, Muratore et al., 2021) and Neural Posterior Domain Randomization (NPDR, Muratore et al., 2022). Additional approaches can be found in S. Chen et al.(2024), Justesen et al. (2018), and Mozian et al. (2020).

All three techniques require a tool for randomizing the generation of environments in a parameterizable way. At the current state of development, PITA is Uniform Domain Randomization compatible or can be seen as a generalized form of it, as it provides more than just uniform distributions for sampling. Further, PITA can be easily extended to support Automatic or Guided Domain Randomization.

3. PITA - Procedural and Iterative Terrain Assembly

In this section, we explain our motivation for developing PITA and provide an overview of its core features. The PITA algorithm is an automated, modular, and randomized 3D world generator designed specifically for MuJoCo-based simulations in Reinforcement Learning. The algorithm’s goal is to simplify and speed up the process of creating environments while aiming to address the problem of overfitting and facilitating generalization.

3.1 Motivation

Physics engines such as MuJoCo, Unity, or PyBullet enable an approximate simulation of physical systems like the real world and serve as a fundamental basis for robotics and RL research. Specifically, MuJoCo is one of the most popular simulation and test environments for state-of-the-art research in these domains (e.g., Akkaya et al., 2019; Andrychowicz et al., 2020; Baker et al., 2020; Körber et al., 2021) due to being fast and accurate. With its acquisition by Google DeepMind in 2021 and the associated free availability, as well as its open sourcing in 2022, the accessibility and popularity have even increased (Kaup et al., 2024). MuJoCo models are written as XML files in their own scene description language called MJCF (DeepMind, 2024). Although the hierarchical arrangement of the nested XML tree is intended for human readability, it can quickly lead to very convoluted files that are difficult to understand and cumbersome to handle. Especially for more complex tasks, such as the creation of numerous diverse levels or larger simulation environments, the manual workflow quickly becomes tedious. MuJoCo can also be accessed programmatically via the dm_control ⁴ software package by Google DeepMind (Tassa et al., 2020), which, among other features, contains a library for compiling and modifying MJCF models with Python (dm_control.mjcf). Unfortunately, these Python bindings lack adequate documentation, requiring users to have sophisticated programming knowledge. Some functions can only be found inside the corresponding GitHub repository, further increasing the required time and effort. To this date, no tool like PITA exists for simulations with MuJoCo, that alleviates the aforementioned problems.

3.2 The PITA Algorithm

The PITA algorithm was developed to make the process of creating environments more accessible and reliable while providing fine-grained control over the generation process. Building directly on top of dm_control, PITA takes on the burden of manually handling the Python bindings and XML files while ensuring that valid models are created without the need for programming knowledge. The user can define the size of the environment, divide it into sub-areas, and determine the number and type of objects to be placed using a simple YAML file. The algorithm’s built-in validation function then verifies that fixed or randomly placed objects do not collide with each other or the plane. Once the generation process is complete, a single XML file is output, which can be loaded into MuJoCo and used as the basis for RL simulations. An example instance of an environment generated with PITA can be seen in Figure 1.

An environment instance generated using PITA.

3.2.1 YAML Configuration

The use of YAML configuration files facilitates the creation of environments with PITA without requiring the users to have any specific background knowledge. YAML, short for YAML Ain’t Markup Language, is a data serialization language characterized by a key-value syntax, which makes it common for configuration files, human-readable, and easily accessible. Figure 2 shows an example of such a configuration file. They can be short and comprehensive for simple environments but also enable users to make a wide range of optional customizations. Notably, each YAML configuration can be interpreted as a distribution over levels. A run of PITA then relates to sampling a level from this distribution with the given seed.

Figure 2: Example YAML configuration.

3.2.2 Assets

Assets are representations of objects that can be placed via PITA and are defined as individual XML files in MuJoCo’s MJCF format. Common objects such as primitive shapes (e.g., spheres or cubes) or light sources are already included in PITA, as well as some showcase objects with more complex shapes (e.g., agents). Users can integrate custom objects by creating corresponding XML files and adding them to the algorithm’s asset folder. MuJoCo also supports the rendering of meshes, an object representation consisting of a collection of vertices and polygons for more complex 3D shapes. In order to be displayed, a mesh file must be contained in the object’s XML file and referenced correctly. This allows, for example, the integration of 3D objects from asset stores such as Unity, Unreal Engine, or comparable 3D simulation frameworks. A large number of these are available online, often under free licenses. However, files must be converted to MuJoCo readable formats such as .obj, .stl, or .msh. Textures can optionally be included as .png files.

3.2.3 Global and Local Placement

Placing objects with PITA can be done in two ways: globally and locally. On the global level, placement of objects is possible throughout the entire environment using relative coordinates. The local level, on the other hand, can be seen as an analogy to biomes in the real world. Using PITA’s Layout Manager, the environment can be divided into a given amount of areas with equal surface area. While functionally identical to the entire environment, they allow the user to, for example, create a forest biome next to a desert or a flower meadow.

3.2.4 Randomization and Distributions

To quickly generate diverse levels, randomization is essential. PITA has incorporated this principle in various ways. For instance, the level size can be sampled on a continuous scale, and meshes may be allocated random positions in the same fashion. Additionally, mesh types can be sampled (e.g., pine or birch tree). Primitives allow for the highest degree of randomization as their color, size, position, and type attributes can be manipulated. For further customization, we implemented several distributions that can be used to sample any object’s x and y coordinates. Among these are Multivariate Uniform, Circular Uniform, Multivariate Normal, and Random Walk distributions. For reproducibility, any non-deterministic part of the algorithm can be controlled by passing a seed to the PITA algorithm. Conveniently, this can be used to create train-test-validation splits by providing disjunct sets of seeds.

3.2.5 Validation

To ensure that user-specified and randomly sampled placement of objects satisfies a customizable set of constraints, we have developed a system of validators and rules. In general, the arrangement of objects on the global level is validated before that on the local level. Contradicting configurations of fixed placement objects result in an error message since the user is required to provide a valid configuration file, while random positioning is retried up to a certain amount of times before an error is thrown. Via the YAML configuration, we allow users to specify rules the validators employ for checking position allocation. Currently implemented are the following rules: Boundary rule (verifies objects are within boundaries), Height rule (verifies objects are above a certain height), Minimum Distance rule (approximate but fast), and Minimum Distance Physics Rule (precise but slow).

3.2.6 JSON Export

In addition to the XML output file, PITA creates an accompanying JSON file that contains relevant information about the created environment instance. Besides the global configuration parameters, each placed object, whether globally or in an area, is mapped to a uniquely identifiable name. All object properties (i.e., name, type, class, position, color, size, and tags) are extracted and stored under the corresponding identifier in the JSON file. RL algorithms can use this mapping to access values that have been assigned to relevant objects, such as agents or targets, during the simulation.

4. Evaluation

To quantify the usefulness of PITA, we set up an extensive evaluation scheme. The main objective is to show the effect of randomization with respect to combating overfitting and facilitating generalization, all while removing the necessity of hand-crafting training levels. We investigate the following hypotheses:

HYP. 1

: An increase in available training levels positively correlates with the RL agent’s ability to generalize.

HYP. 2

: The fewer training levels available, the quicker the agent overtrains, hence diminishing generalization capabilities.

The experiments were designed to test the aforementioned hypotheses in a controlled setup that maintains simplicity yet operates in a sophisticated simulation. The simplicity was intentionally chosen to ensure that we solely capture the hypothesized phenomena without potential confounds. The setup consists of a squared, flat plane with borders, an agent, a distractor, and a target (see Figure 3 for an example level). The agent is tasked with navigating to the target as quickly as possible without colliding with the borders or the distractor. In order to cover a wide range of different amounts of levels, we generated 100 versions of this fairly simple environment, seeded by their index. We chose to train the agent on subsets consisting of 1, 5, 10, 25, 50, and 100 levels, respectively. To mitigate the inherently high variance of Reinforcement Learning, we repeat each experiment condition ten times.

Figure 3: A top-down (left) and the respective agent view (right) for an example level.

4.1 Methodology

In the following we describe our methodological setup by detailing the architecture used, the training process, and defining hyperparameters before concluding on the evaluation metrics employed.

4.1.1 Architecture

We use the Proximal Policy Optimization (PPO, ) implementation of Stable Baselines 3 (SB3) v2.0.0 ⁵ for our experiments with custom Multilayer Perceptron (MLP) value and policy networks. Both MLPs are initialized as a three-layer neural network with 512, 256, and 128 neurons, respectively, a tanh activation function, and no shared layers.

The observation space consists of a 64-dimensional vector, being a compressed version of a 64 x 64 pixel RGB image rendered from the agent’s 1st person perspective within the MuJoCo engine. Our implementation considers the image compression step as part of the environment dynamics. It is performed by the encoder network of a pre-trained Autoencoder (AE) the weights of which are frozen during the experiments. Inherently, the encoder is a four-layer neural network consisting of two convolutional layers, a flattening layer, and a linear readout layer. Both convolutional layers, as well as the linear layer, are ReLU-activated. During pre-training, the AE’s decoder is tasked with reconstructing the original image. The corresponding network combines a ReLU-activated linear layer and two transposed convolutional layers, with the latter using a sigmoid activation function to generate pixel values between 0 and 1. Using a pre-trained AE is intended to facilitate learning during our RL experiments by giving the agent access to a computationally easier-to-interpret input space. This way, the essential information of the visual space is preserved while reducing the dimensionality of the image information. Additionally, the reconstruction task is independent of the navigation task, which is in contrast to an encoding that, e.g., explicitly encodes the position of targets or distractors.

4.1.2 Training and Hyperparameters

All relevant training hyperparameters were determined via a manual grid search. For the Autoencoder training dataset, we captured 10k images by randomly navigating the agent through all 100 levels. Afterward, we trained the model until convergence using the parameters reported in Table 1.

Table 1. Hyperparameters for AE Training

To subsequently train the agent PPO network, we implemented the trained AE as a visual preprocessing unit. The actions available to the agent lie on a continuous scale in the interval [-1,1] and include rotating left-right and moving forwards-backwards as well as sideways.

Furthermore, careful consideration was given to incentivizing desirable behaviors while punishing counterproductive actions. Formally, the reward function R_t can be defined as:

R_t = R_time,t + R_distance,t + R_success,t

Where:

with D_t being the distance between agent and target at timestep t. Penalties were applied for hitting borders or distractors, both of which resulted in a -1 reward, and ending the episode. In addition, a subtle time penalty of -0.0001 per step has been implemented to encourage efficiency. Moving away from the target also incurs a penalty equal to the distance traveled compared to the previous step. To reinforce positive learning, rewards were given for hitting the target (+1) and advancing towards it. The rewards given for the change of distance between the agent and the target serve the purpose of countering the sparse reward problem, which is commonly encountered in RL.

In addition, we applied frame skipping and frame stacking, as consecutive frames are highly correlated. This effectively gives the agent a primitive form of short-term memory. By repeating each action over 60 frames and passing the last five frames to the visual preprocessing stage as stacked 5x64x64x3 images, we can hence speed up the training. A list of all PPO-related hyperparameters can be found in Table 2.

4.1.3 Evaluation Metrics

For the experiment, we employed several key metrics to gain comprehensive insights. These metrics encompass success rate, mean episode length, and mean reward evaluated on both train and test sets. Values were recorded after each episode during training. The first metric is concerned with the ratio of successfully completed episodes. It provides a robust measure of overall task performance with a focus on task completion. The mean episode length depicts the steps needed to end an episode regardless of the outcome.

Table 2 Hyperparameters for PPO Training

Combined with the success rate, this metric indicates the efficiency of task accomplishment. Lastly, the mean reward describes the cumulative reward over episodes, serving as another fundamental gauge of learning success.

4.2 Results

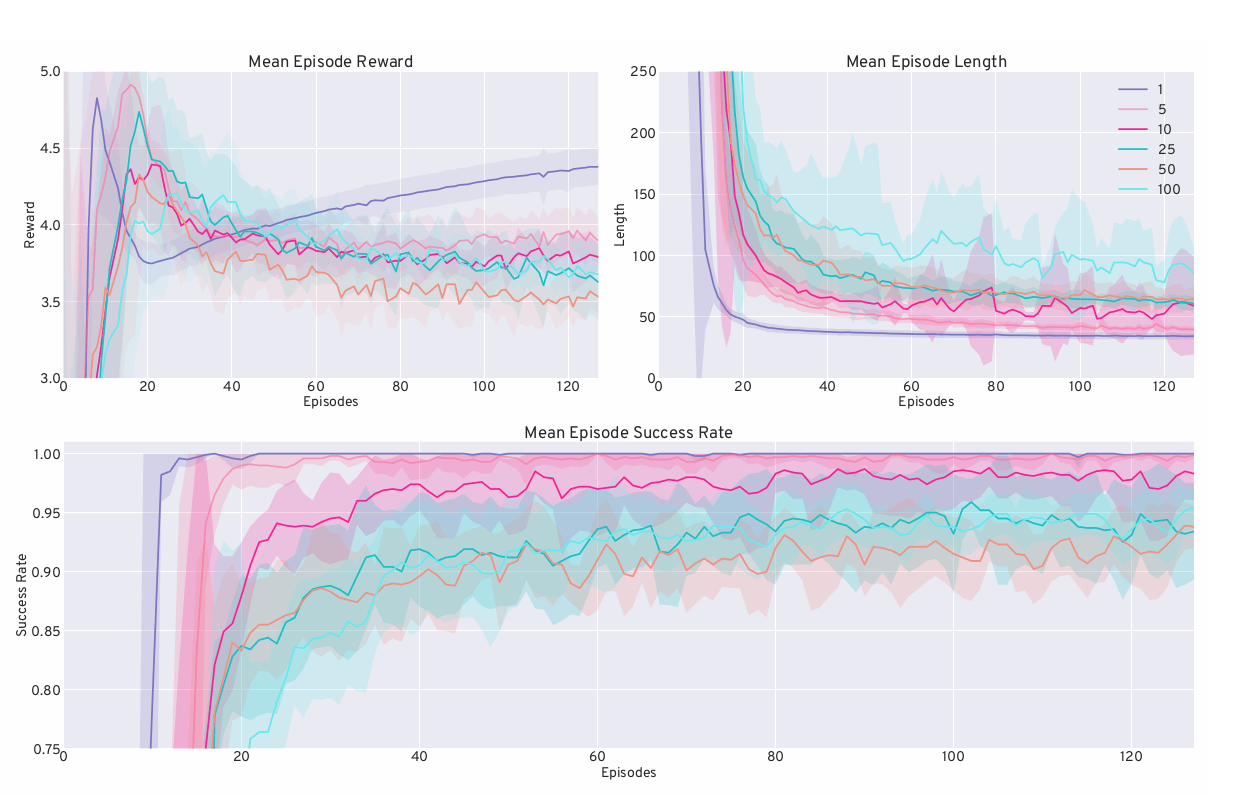
Our experiments demonstrate successful convergence on the training data with respect to mean success rate, mean episode length, and mean episode reward (see Figure 4). Generally, performance on all three metrics is best with one training level and decreases as the number of available training levels increases, albeit not always in a consistently rising order. When comparing the last 10% of training between the worst and best conditions, we have observed differences of approximately 6.7% in the success rate, 56 steps in episode length, and a discrepancy of around 0.84 points in reward. These rather small variations lead to large overlaps of the 68% confidence intervals.

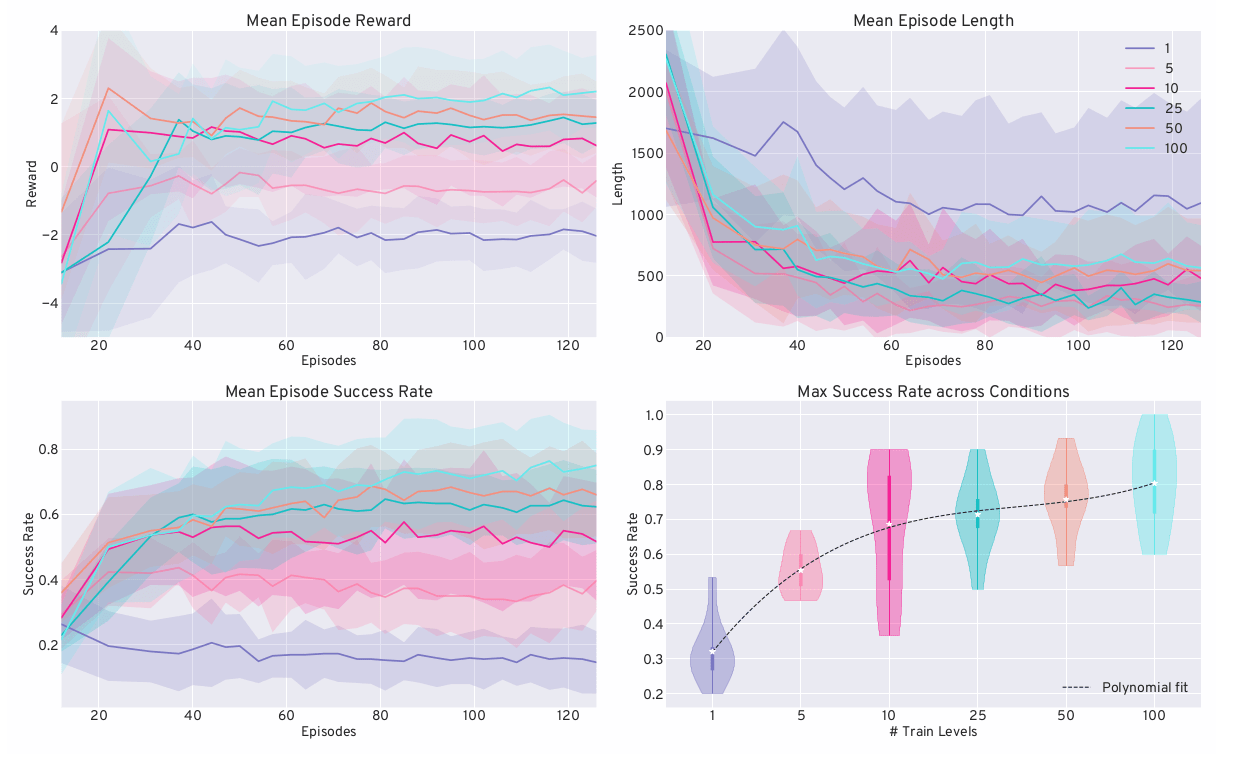
Figure 5 illustrates the test results per condition over 30 held-out test levels. For the mean episode reward (top left), length (top right), and success rate (bottom left), the respective metrics are shown with their 68% confidence intervals, while the peak success rate (bottom right) is depicted as a violin plot. In contrast to training, the average episode reward increases with the number of available levels, with the one-level condition having the lowest value. Notably, there is a clear upward trend in the mean and peak success rate and mean reward per condition, with diminishing differences between 10, 25, 50, and 100 levels. Meanwhile, the mean episode length during testing exhibits an ambiguous ordering. Overall, one can see differences of roughly 57.4% in the success rate, 779 steps in the episode length, and 4.01 points in the reward per episode (last 10% of evaluation values).

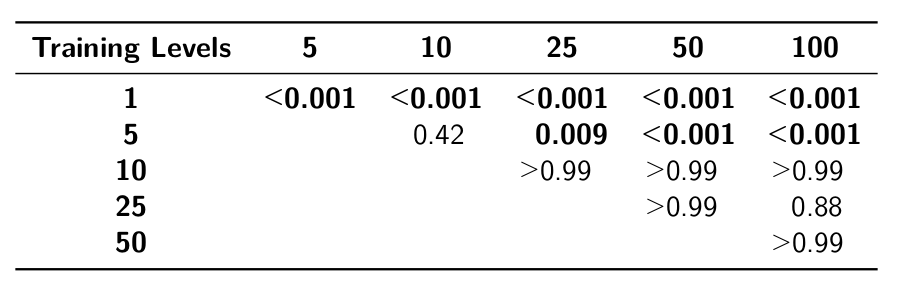
Performance metrics on held-out evaluation levels per condition. The line plots depict the corresponding mean value over all repetitions, along with their 68% confidence intervals. Additionally, a violin plot visualizes the max success rate across all conditions and repetitions. The polynomial fit exhibits a monotonic increase in mean max success rates.

Although the differences in peak success rate between the 5 and 10, as well as the 10 and above level conditions, are not statistically significant (Table 3), a correlation between available training levels and test performance can still be seen. This is highlighted by a monotonic increase in mean peak success rates. It should be pointed out that the significance tests were, to a large degree, driven by the high variance of the sample for the 10-level condition. For the other conditions, the variance is markedly more comparable.

5. Discussion

We confirm that all agents successfully learned to finish their given levels based on their close-to-perfect train success rates. The comparatively small differences between the conditions during training prove that we have designed a basic experiment that can be solved easily even as variation increases with the number of levels.

Figure 4: Performance metrics on training levels per condition. The plots depict the corresponding mean value over all repetitions, along with their 68% confidence intervals.

Performance on the held-out test data revealed more pronounced differences. In light of our hypotheses, we can indeed see a correlation between the number of available training levels and the generalization capabilities of the agents (Hypothesis 1). With more available training levels, agents show a clear tendency to solve more test levels, usually in a faster manner, which is also reflected in higher average episode rewards. This is further emphasized by the peak success rate plot (Figure 5) with its monotonically increasing polynomial fit, albeit with non-significant p-values in some conditions (see Table 3).

Table 3: P-values of one-sided t-tests for the hypotheses H_j,k := SR_j < SR_k with SR_j and SR_k being the success rates for two given conditions. The reported p-values are Bonferroni corrected, hence any p-value below the chosen significance level of α = 0.05 (bold entries in the table) can be interpreted as rejecting the joint overall null hypothesis that contrasts Hypothesis 1.

This finding is in line with the results from Zhang et al. (2018) and extends them to the domain of complex simulation in MuJoCo. However, an increase in levels also entails higher resource costs due to more prolonged training and evaluation times. Therefore, it is essential to weigh up the additional benefits against these expenses, particularly considering the diminishing returns we have observed in our simplified environment.

Figure 5: Performance metrics on held-out evaluation levels per condition. The line plots depict the corresponding mean value over all repetitions, along with their 68% confidence intervals. Additionally, a violin plot visualizes the max success rate across all conditions and repetitions. The polynomial fit exhibits a monotonic increase in mean max success rates.

Concerning Hypothesis 2, we can also confirm that the fewer levels available, the faster an overtraining effect occurs. This is supported by an on-average decline in both evaluation success rates and episode rewards for the conditions ≤ 10 and ≤ 5 levels, respectively. From episode 50 onward, individual runs illustrate this phenomenon well, while on average, it rather remains a tendency. Using drops in training performance as an early stop criterion, however, can not solve this problem, as agents have usually not converged on the train set then. The most pronounced downward trend can be seen with a single level.

When viewing the performance of the PITA algorithm in light of these results, we see that we were able to quantify its usefulness successfully. The rapid generation of environment instances allowed us to accumulate a significant number of levels, which in turn showed substantial benefits for training. In particular, we observed improved generalization capabilities on the test set as the number of training levels increased. However, our analysis revealed diminishing returns, evidenced by non-significant p-values for the 5 and 10-level t-test, as well as all combinations with 10 levels and above. This phenomenon is likely driven by the deliberate simplicity of our environment, in which the available variety of levels and significantly different observations for the agent are quickly exhausted. We conjecture that this effect may occur later in more complex environments, as agents would receive a greater diversity of observations from more varied levels, thus delaying the onset of diminishing returns.

While PITA is not a benchmark for RL such as Albrecht et al. (2022) , Cobbe et al. (2020), Dai 12Cognitive Science Student Journal 2024, 8 Bartels, Dudek, Frommelt, Blanke & Keffer et al. (2022), Juliani et al. (2019) , and Kanagawa and Kaneko (2019), we demonstrated how to use it to create benchmarks on the fly, exemplified by our simple navigation task. Additionally, PITA is set apart from other Domain Randomization tools, such as the ones presented in Johansen et al. (2019) and Samvelyan et al. (2021), by giving access to complex simulations in 3D environments.

Despite the significant insights we gained from our experiment, two limitations are worth noting. First, the limitation imposed by the available hardware prevented us from including more evaluation levels that would have allowed a more comprehensive understanding of agent performance. Second, a higher number of repetitions would have been beneficial as it would likely have mitigated the effects of outliers, like those in the 10-level condition. A larger sample size might have provided a more robust and reliable assessment of the agent’s abilities in different conditions, thus increasing the overall validity of our results.

For future work, we suggest investigating the effect of available training levels on test performance with aforementioned environments of increased complexity. Together with the results described here, this would provide a more well-rounded answer to whether PITA aids generalization in Reinforcement Learning. Since PITA comes with the necessary tools for Uniform Domain Randomization, it can fairly easily be extended to Domain Transfer with automatic or guided DR approaches, as in Akkaya et al. (2019), S. Chen et al. (2024), Gur et al. (2021), Mehta et al. (2020), Mozian et al. (2020), Muratore et al. (2022), and Wang et al. (2020). Test sets from new domains can be implemented by sampling from YAML configurations that are different from the ones used for generating training data. Furthermore, we encourage researchers from diverse domains within embodied RL to utilize PITA to speed up their environment design and level generation process. Simultaneously, we aspire to gather new requirements through external feedback to facilitate ongoing enhancements to the PITA algorithm. Regarding PITA itself, our agenda is to enrich its feature set continuously. With the next major release, we plan to add an intuitive user interface, obviating the need for direct engagement with YAML files. Furthermore, the update will introduce the capacity for customization through custom callbacks alongside an expanded asset library. Finally, we want to add the concept of subareas to PITA. This will enable the user to create overlapping regions within an area, thereby facilitating more nuanced and precise control.

6. Conclusion

In this paper, we have introduced the PITA algorithm as a Domain Randomization tool in RL to facilitate generalization capabilities while simplifying the creation of complex environments in the first place. By creating an experimental setup and comparing different conditions with increasing available training levels, we have shown PITA’s usefulness with a clearly measurable incline in the generalization capabilities of the corresponding agent. All selected evaluation metrics reflected that the amount of available training levels correlates positively with test performance, while the differences between conditions become progressively smaller. We argue that the latter results from the variety of observations made by the agent, which was limited by our purposely chosen basic configuration. Especially for more complex environments, we expect the observed saturation effect to set in later due to a greater variety of levels and observations. This would simultaneously lead to a more pronounced difference and increased generalization. Hence, we were able to directly demonstrate PITA’s raison d’être as a randomization tool for RL researchers and other disciplines requiring Domain Randomization in MuJoCo. While it has yet to establish itself as a proper tool in the research community after the upcoming release, we strive to further improve accessibility and usability by continuously developing and integrating new features.

References

Akkaya, Ilge, Marcin Andrychowicz, Maciek Chociej, Mateusz Litwin, Bob McGrew, Arthur Petron, Alex Paino, et al. 2019. “Solving Rubik’s Cube with a Robot Hand.” arXiv. https://doi.org/10.48550/arXiv.1910.07113.

Albrecht, Joshua, Abraham Fetterman, Bryden Fogelman, Ellie Kitanidis, Bartosz Wróblewski, Nicole Seo, Michael Rosenthal, et al. 2022. “Avalon: A Benchmark for RL Generalization Using Procedurally Generated Worlds.” Advances in Neural Information Processing Systems 35: 12813–25. https://proceedings.neurips.cc/paper_files/paper/2022/hash/539f1f7dd156cfe1222b0be83f247d35-Abstract-Datasets_and_Benchmarks.html.

Andrychowicz, OpenAI: Marcin, Bowen Baker, Maciek Chociej, Rafal Józefowicz, Bob McGrew, Jakub Pachocki, Arthur Petron, et al. 2020. “Learning Dexterous in-Hand Manipulation.” The International Journal of Robotics Research 39 (1): 3–20. https://doi.org/10.1177/0278364919887447.

Baker, Bowen, Ingmar Kanitscheider, Todor Markov, Yi Wu, Glenn Powell, Bob McGrew, and Igor Mordatch. 2020. “Emergent Tool Use From Multi-Agent Autocurricula.” arXiv. https://doi.org/10.48550/arXiv.1909.07528.

Bellemare, M. G., Y. Naddaf, J. Veness, and M. Bowling. 2013. “The Arcade Learning Environment: An Evaluation Platform for General Agents.” Journal of Artificial Intelligence Research 47: 253–79. https://doi.org/10.1613/jair.3912.

Chen, Shutong, Guanjun Liu, Ziyuan Zhou, Kaiwen Zhang, and Jiacun Wang. 2024. “Robust Multi-Agent Reinforcement Learning Method Based on Adversarial Domain Randomization for Real-World Dual-UAV Cooperation.” IEEE Transactions on Intelligent Vehicles 9 (1): 1615–27. https://doi.org/10.1109/TIV.2023.3307134.

Chen, Xiaoyu, Jiachen Hu, Chi Jin, Lihong Li, and Liwei Wang. 2022. “Understanding Domain Randomization for Sim-to-Real Transfer.” In. https://doi.org/10.48550/arXiv.2110.03239.

Cobbe, Karl, Chris Hesse, Jacob Hilton, and John Schulman. 2020. “Leveraging Procedural Generation to Benchmark Reinforcement Learning.” In Proceedings of the 37th International Conference on Machine Learning, 2048–56. PMLR. https://proceedings.mlr.press/v119/cobbe20a.html.

Cobbe, Karl, Oleg Klimov, Chris Hesse, Taehoon Kim, and John Schulman. 2019. “Quantifying Generalization in Reinforcement Learning.” In Proceedings of the 36th International Conference on Machine Learning, 1282–89. PMLR. https://proceedings.mlr.press/v97/cobbe19a.html.

Dai, Tianhong, Kai Arulkumaran, Tamara Gerbert, Samyakh Tukra, Feryal Behbahani, and Anil Anthony Bharath. 2022. “Analysing Deep Reinforcement Learning Agents Trained with Domain Randomisation.” Neurocomputing 493: 143–65. https://doi.org/10.1016/j.neucom.2022.04.005.

DeepMind, Technologies Limited. 2024. “MuJoCo Documentation.” https://mujoco.readthedocs.io/en/stable/overview.html.

Foerster, Jakob, Ioannis Alexandros Assael, Nando de Freitas, and Shimon Whiteson. 2016. “Learning to Communicate with Deep Multi-Agent Reinforcement Learning.” In Advances in Neural Information Processing Systems, edited by D. Lee, M. Sugiyama, U. Luxburg, I. Guyon, and R. Garnett. Vol. 29. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2016/file/c7635bfd99248a2cdef8249ef7bfbef4-Paper.pdf.

Fujimoto, Scott, Herke Hoof, and David Meger. 2018. “Addressing Function Approximation Error in Actor-Critic Methods.” In Proceedings of the 35th International Conference on Machine Learning, 1587–96. PMLR. https://proceedings.mlr.press/v80/fujimoto18a.html.

Gur, Izzeddin, Natasha Jaques, Yingjie Miao, Jongwook Choi, Manoj Tiwari, Honglak Lee, and Aleksandra Faust. 2021. “Environment Generation for Zero-Shot Compositional Reinforcement Learning.” In Advances in Neural Information Processing Systems, edited by M. Ranzato, A. Beygelzimer, Y. Dauphin, P. S. Liang, and J. Wortman Vaughan, 34:4157–69. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2021/file/218344619d8fb95d504ccfa11804073f-Paper.pdf.

Haarnoja, Tuomas, Aurick Zhou, Pieter Abbeel, and Sergey Levine. 2018. “Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor.” In Proceedings of the 35th International Conference on Machine Learning, 1861–70. PMLR. https://proceedings.mlr.press/v80/haarnoja18b.html.

Johansen, Mads, Martin Pichlmair, and Sebastian Risi. 2019. “Video Game Description Language Environment for Unity Machine Learning Agents.” In 2019 IEEE Conference on Games (CoG), 1–8. https://doi.org/10.1109/CIG.2019.8848072.

Juliani, Arthur, Ahmed Khalifa, Vincent-Pierre Berges, Jonathan Harper, Ervin Teng, Hunter Henry, Adam Crespi, Julian Togelius, and Danny Lange. 2019. “Obstacle Tower: A Generalization Challenge in Vision, Control, and Planning,” 2684–91. https://www.ijcai.org/proceedings/2019/373.

Justesen, Niels, Ruben Rodriguez Torrado, Philip Bontrager, Ahmed Khalifa, Julian Togelius, and Sebastian Risi. 2018. “Illuminating Generalization in Deep Reinforcement Learning Through Procedural Level Generation.” arXiv. https://doi.org/10.48550/arXiv.1806.10729.

Kanagawa, Yuji, and Tomoyuki Kaneko. 2019. “Rogue-Gym: A New Challenge for Generalization in Reinforcement Learning.” In 2019 IEEE Conference on Games (CoG), 1–8. https://doi.org/10.1109/CIG.2019.8848075.

Kaup, Michael, Cornelius Wolff, Hyerim Hwang, Julius Mayer, and Elia Bruni. 2024. “A Review of Nine Physics Engines for Reinforcement Learning Research.” arXiv. https://doi.org/10.48550/arXiv.2407.08590.

Kontes, Georgios D., Daniel D. Scherer, Tim Nisslbeck, Janina Fischer, and Christopher Mutschler. 2020. “High-Speed Collision Avoidance Using Deep Reinforcement Learning and Domain Randomization for Autonomous Vehicles.” In 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), 1–8. https://doi.org/10.1109/ITSC45102.2020.9294396.

Körber, Marian, Johann Lange, Stephan Rediske, Simon Steinmann, and Roland Glück. 2021. “Comparing Popular Simulation Environments in the Scope of Robotics and Reinforcement Learning.” arXiv. https://doi.org/10.48550/arXiv.2103.04616.

Lanctot, Marc, Vinicius Zambaldi, Audrunas Gruslys, Angeliki Lazaridou, Karl Tuyls, Julien Perolat, David Silver, and Thore Graepel. 2017. “A Unified Game-Theoretic Approach to Multiagent Reinforcement Learning.” In Advances in Neural Information Processing Systems, edited by I. Guyon, U. Von Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett. Vol. 30. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2017/file/3323fe11e9595c09af38fe67567a9394-Paper.pdf.

Mehta, Bhairav, Manfred Diaz, Florian Golemo, Christopher J. Pal, and Liam Paull. 2020. “Active Domain Randomization.” In Proceedings of the Conference on Robot Learning, 1162–76. PMLR. https://proceedings.mlr.press/v100/mehta20a.html.

Mordatch, Igor, and Pieter Abbeel. 2018. “Emergence of Grounded Compositional Language in Multi-Agent Populations.” Proceedings of the AAAI Conference on Artificial Intelligence 32 (1). https://doi.org/10.1609/aaai.v32i1.11492.

Mozian, Melissa, Juan Camilo Gamboa Higuera, David Meger, and Gregory Dudek. 2020. “Learning Domain Randomization Distributions for Training Robust Locomotion Policies.” In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 6112–17. https://doi.org/10.1109/IROS45743.2020.9341019.

Muratore, Fabio, Christian Eilers, Michael Gienger, and Jan Peters. 2021. “Data-Efficient Domain Randomization With Bayesian Optimization.” IEEE Robotics and Automation Letters 6 (2): 911–18. https://doi.org/10.1109/LRA.2021.3052391.

Muratore, Fabio, Theo Gruner, Florian Wiese, Boris Belousov, Michael Gienger, and Jan Peters. 2022. “Neural Posterior Domain Randomization.” In Proceedings of the 5th Conference on Robot Learning, 1532–42. PMLR. https://proceedings.mlr.press/v164/muratore22a.html.

Risi, Sebastian, and Julian Togelius. 2020. “Increasing Generality in Machine Learning Through Procedural Content Generation.” Nature Machine Intelligence 2 (8): 428–36. https://doi.org/10.1038/s42256-020-0208-z.

Rita, Mathieu, Corentin Tallec, Paul Michel, Jean-Bastien Grill, Olivier Pietquin, Emmanuel Dupoux, and Florian Strub. 2022. “Emergent Communication: Generalization and Overfitting in Lewis Games.” In Advances in Neural Information Processing Systems, edited by S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh, 35:1389–1404. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2022/file/093b08a7ad6e6dd8d34b9cc86bb5f07c-Paper-Conference.pdf.

Russell, Stuart J., and Peter Norvig. 2020. Artificial Intelligence: A Modern Approach. 4th ed. Pearson.

Samvelyan, Mikayel, Robert Kirk, Vitaly Kurin, Jack Parker-Holder, Minqi Jiang, Eric Hambro, Fabio Petroni, Heinrich Kuttler, Edward Grefenstette, and Tim Rocktäschel. 2021. “MiniHack the Planet: A Sandbox for Open-Ended Reinforcement Learning Research.” In Proceedings of the Neural Information Processing Systems Track on Datasets and Benchmarks, edited by J. Vanschoren and S. Yeung. Vol. 1. Curran. https://doi.org/10.48550/arXiv.2109.13202.

Schulman, John, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. “Proximal Policy Optimization Algorithms.” arXiv. https://doi.org/10.48550/arXiv.1707.06347.

Tassa, Yuval, Saran Tunyasuvunakool, Alistair Muldal, Yotam Doron, Piotr Trochim, Siqi Liu, Steven Bohez, et al. 2020. “Dm_control: Software and Tasks for Continuous Control.” Software Impacts. https://doi.org/10.1016/j.simpa.2020.100022.

Todorov, Emanuel, Tom Erez, and Yuval Tassa. 2012. “MuJoCo: A Physics Engine for Model-Based Control.” In 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 5026–33. https://doi.org/10.1109/IROS.2012.6386109.

WANG, KAIXIN, Bingyi Kang, Jie Shao, and Jiashi Feng. 2020. “Improving Generalization in Reinforcement Learning with Mixture Regularization.” In Advances in Neural Information Processing Systems, edited by H. Larochelle, M. Ranzato, R. Hadsell, M. F. Balcan, and H. Lin, 33:7968–78. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2020/file/5a751d6a0b6ef05cfe51b86e5d1458e6-Paper.pdf.

Wang, Rui, Joel Lehman, Aditya Rawal, Jiale Zhi, Yulun Li, Jeffrey Clune, and Kenneth Stanley. 2020. “Enhanced POET: Open-Ended Reinforcement Learning Through Unbounded Invention of Learning Challenges and Their Solutions.” In Proceedings of the 37th International Conference on Machine Learning, 9940–51. PMLR. https://proceedings.mlr.press/v119/wang20l.html.

Wang, Yaqing, Quanming Yao, James T. Kwok, and Lionel M. Ni. 2020. “Generalizing from a Few Examples: A Survey on Few-Shot Learning.” ACM Computing Surveys 53 (3): 63:1–34. https://doi.org/10.1145/3386252.

Weng, Lilian. 2019. “Domain Randomization for Sim2Real Transfer.” https://lilianweng.github.io/posts/2019-05-05-domain-randomization/.

Zhang, Chiyuan, Oriol Vinyals, Remi Munos, and Samy Bengio. 2018. “A Study on Overfitting in Deep Reinforcement Learning.” arXiv. https://doi.org/10.48550/arXiv.1804.06893.

Research question

On the one hand, the paper presents PITA as a tool. On the other hand, we designed an experiment to serve as a proof of concept for PITA, i.e., showcasing its usefulness in mitigating overfitting / improving generalization in Reinforcement Learning.